In the past few decades, researchers specializing in condensed matter physics have been intensely interested in studying the properties of strongly correlated quantum many-body systems, which are systems on the microscopic scale that include more than two particles that interact with each other. Researchers especially want to be able to explain how the macroscopic behavior of materials can be explained by the fundamental interactions of the material’s microscopic constituents.
Particular interest has focused on quantum spin-lattice systems, where the interactions can be simply described, but where different types of interaction can compete with one another. (The “spin” of an elementary particle is an inherent property it possesses in quantum mechanics that has no classical counterpart, although it can loosely be thought of as a form of internal angular momentum. In a standard computational model in condensed matter physics, these spins are arranged on a lattice and coupled through magnetic interactions.) The system can then find itself in a frustrated state in which different forms of ordering are trying to emerge in competition with one another. The often subtle interplay between this frustration and quantum fluctuations can lead to quantum spin-lattice models exhibiting ground-state (i.e., at zero temperature) phase diagrams that are very different from their classical counterparts. Of greatest theoretical interest are the so-called quantum critical points where phase transitions occur.
Computer models for quantum-mechanical wave functions of strongly interacting many-spin systems are extremely complex. This is especially so near the quantum critical points, where the ground-state phase has special properties and involves a very large set of fluctuating configurations. Methods for modeling these systems have included techniques from quantum field theory or large-scale numerical simulations such as Monte Carlo methods. Since the effects of quantum fluctuations, and hence the complexity of the wave functions, increase the closer one approaches the quantum critical points, very accurate quantum many-body techniques are necessary.
Professor Charles Campbell (Physics and Astronomy) and his colleagues Professor Raymond Bishop and Dr. Peggy Li at the University of Manchester (UK), and their collaborators elsewhere, have developed and adapted one such many-body method, the so-called coupled cluster method (CCM), to study a large and diverse array of two-dimensional (2D) quantum spin systems of theoretical and experimental interest. The CCM is now widely accepted as being one of the most successful and most widely applicable of all modern methods of microscopic quantum many-body theory. The CCM techniques pioneered by Professor Bishop and his collaborators are probably now the best available for these strongly frustrated 2D quantum spin-lattice systems, and their results are now setting benchmarks in the field. The group runs their CCM codes on MSI’s supercomputers. The interesting magnetic phenomena displayed by such systems make them suitable candidates for a large number of technological applications, many of which are already in widespread use. This research is also providing insights into exciting new systems, such as exotic superconducting systems and non-superconducting systems that have unusual magnetic properties.
Professor Bishop’s contributions to the development and applications of the CCM resulted in his sharing the Eugene Feenberg Memorial Medal in 2005. (The Feenberg Medal is awarded for work that significantly advances the field of many-body physics.) His co-recipient, the late Hermann Kuemmel, is generally acknowledged as the inventor of the CCM. Among other contributions, Professor Bishop has adapted the CCM to several important quantum many-body systems, including the quantum magnetism problems described above. Professor Campbell, who is a long-time researcher at MSI in the field of quantum fluid research, has been working with Professor Bishop and his former student and now post-doctoral associate Dr. Li, adding his own area of expertise to the CCM. Bishop, Li, and Campbell have used MSI resources for several years in their work to advance this technique.
Approximately 10 papers describing this research using MSI have been published since the start of 2012. These have appeared in the journals Physical Review B, Journal of Physics: Condensed Matter, and the European Physical Journal B. Two of the articles were chosen by the editors for special highlighting. The group has especially concentrated on the spin-1/2 J1-J2-J3 model on the honeycomb lattice and the spin-1/2 J1-J2 model on the checkerboard lattice (otherwise known as the anisotropic planar pyrochlore), which have recently become very hot topics in the field.
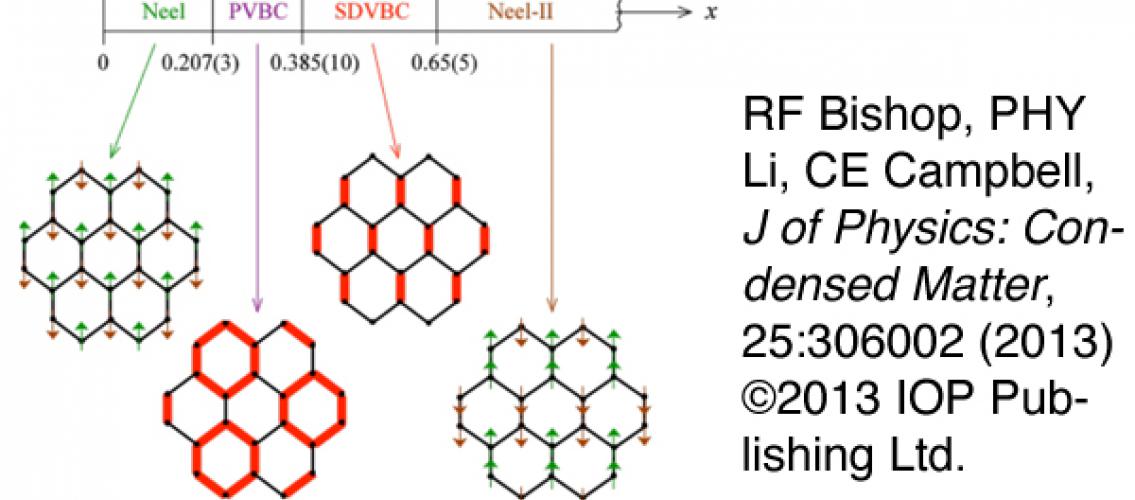
Image Description: Phase diagram of the spin-1/2 J1−J2 model on the honeycomb lattice (with J1 > 0 and x ≡ J2/J1 > 0), as obtained by a CCM analysis. The four phases shown are Néel, plaquette valence-bond crystalline (PVBC), staggered dimer valence-bond crystalline (SDVBC), and Néel-II. The quantum critical points (phase transitions) are at xc1 ≈ 0.207(3), xc2 ≈ 0.385(10), and xc3 ≈ 0.65(5), as shown in the diagram. From “Valence-bond crystalline order in the s = 1/2 J1−J2 model on the honeycomb lattice,” R.F. Bishop, P.H.Y. Li and C.E. Campbell, Journal of Physics: Condensed Matter 25:306002, DOI=10.1088/0953-8984/25/30/306002 (2013) ©2013 IOP Publishing Ltd.
Posted on October 30, 2013.